Enem 2020 - Questão resolvida #06

(Enem 2020) Um mergulhador fica preso ao explorar uma caverna no oceano. Dentro da caverna formou-se um bolsão de ar, como mostrado na figura, onde o mergulhador se abrigou.

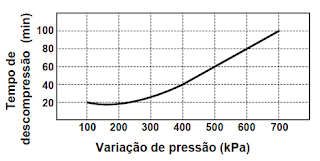
Durante o resgate, para evitar danos a seu organismo, foi necessário que o mergulhador passasse por um processo de descompressão antes de retornar à superfície para que seu corpo ficasse novamente sob pressão atmosférica. O gráfico mostra a relação entre os tempos de descompressão recomendados para indivíduos nessa situação e a variação de pressão.

Considere que a aceleração da gravidade seja igual a $ 10 \ \text{m} \ \text{s}^{-2}$ e que a densidade da água seja de $\rho = 1 000 \ \text{kg} \ \text{m}^{-3}$.

Em minutos, qual é o tempo de descompressão a que o mergulhador deverá ser submetido?

a) 100 b) 80 c) 60 d) 40 e) 20

O princípio fundamental da Hidrostática afirma que, em um líquido, a variação $\Delta p$ de pressão entre dois pontos é igual ao produto entre a densidade $\rho$ do líquido, a aceleração $g$ da gravidade e a distância $\Delta h$ entre essses dois pontos,

\begin{equation} \Delta p = \rho g \, \Delta h \text{.} \end{equation}

Considerando que um dos pontos situa-se na superfície e o outro na profundidade do bolsão, $\Delta h = 50 \ \text{m}$. Com isso, através da Equação (1),

\begin{equation} \begin{split} \Delta p &= \rho g \, \Delta h \\ &= 1000 \cdot 10 \cdot 50 \\ &= 500000 \ \text{Pa} \\ &= 500 \ \text{kPa} \text{.} \\ \end{split} \end{equation}

Assim, ao analisarmos o gráfico do enunciado, o tempo de descompressão para uma variação $\Delta p = 500 \ \text{kPa}$ é de $60 \ \text{min}$.

Resposta: c.

---

Próxima questão >

☰ Índice de questões

< Questão anterior

---