Frações (resumo nível médio)

Fonte: imagem criada no Canva.

Uma fração é uma parte de um todo e, como veremos mais adiante, seu resultado pode sempre ser obtido através de uma simples divisão. Este resumo a nível médio é dedicado às frações e suas operações.

Definição

Quando dividimos uma pizza em oito pedaços, cada parte representa um pedaço de oito. Essas partes são denominadas frações.

Figura 1. Exemplo de uma fração: uma parte em oito.

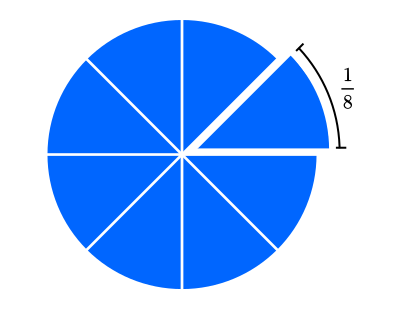
Esse valor pode ser representado como $\frac{1}{8}$ ou $1/8$, onde o primeiro número (o de cima) é chamado de numerador e o outro (o de baixo) de denominador.

\begin{equation} \frac{ \txt{numerador} }{ \txt{denominador} } \end{equation}

O resultado de uma fração é a divisão do numerador pelo denominador. No caso do exemplo da Figura 1:

\begin{align*} \begin{split} \frac{1}{8} &= 1/8 \\ &= 0{,}125 \pt \end{split} \end{align*}

Veja que o denominador não pode ser nulo pois não podemos dividir um número por $0$. 🤷‍♂️

Qualquer número inteiro pode ser escrito em forma de fração se lembrarmos que todo número dividido por $1$ resulta nele mesmo.

Exemplo 1

Note, com este exemplo, que $4$ é o mesmo que $4/1$.

\begin{align*} 4 &= 4/1 \\ &= \frac{4}{1} \end{align*}

Após essa breve definição sobre frações, vamos voltar nossa atenção às operações básicas.

Frações inversas

Para inverter uma fração, troca-se o numerador pelo denominador. O resultado é chamado de inverso ou fração inversa.

Exemplo 2

A fração inversa de $\frac{4}{1}$ é $\frac{1}{4}$.

Exemplo 3

O inverso de $\frac{a}{5}$ é $\frac{5}{a}$.

Frações negativas

Quando o numerador ou o denominador possuir sinal negativo, ele pode ser colocado para fora da fração.

Exemplo 4

As frações abaixo possuem o mesmo resultado:

\begin{equation*} \frac{-4}{21} = -\frac{4}{21} \pt \end{equation*}

Exemplo 5

As frações abaixo possuem o mesmo resultado:

\begin{equation*} \frac{7}{-b} = -\frac{7}{b} \pt \end{equation*}

Exemplo 6

Todas as frações abaixo possuem o mesmo resultado:

\begin{align*} \begin{split} \frac{-b}{-3} &= -\frac{b}{-3} \\ &= -\Big(-\frac{b}{3}\Big) \\ &= \frac{b}{3} \pt \end{split} \end{align*}

Da mesma forma, o sinal que acompanha uma fração também pode ser colocado para dentro.

Exemplo 7

Todas as frações abaixo possuem o mesmo resultado:

\begin{align*} \begin{split} -\frac{a}{b} &= \frac{-a}{b} \\ &= \frac{a}{-b} \pt \end{split} \end{align*}

Multiplicação de frações

Para multiplicar frações, multiplicamos entre si seus numeradores e seus denominadores. O resultado é uma nova fração.

Exemplo 8

Vamos multiplicar a fração $2/3$ pela fração $12/4$:

\begin{align*} \begin{split} \frac{2}{3} \cdot \frac{12}{4} &= \frac{2 \cdot 12}{3 \cdot 4}\\ &= \frac{24}{12} \pt \end{split} \end{align*}

Exemplo 9

Vamos multiplicar o número $5$ pela fração $4/c$:

\begin{align*} \begin{split} 5 \cdot \frac{4}{c} &= \frac{5}{1} \cdot \frac{4}{c} \\ &= \frac{5 \cdot 4}{c} \\ &= \frac{20}{c} \pt \end{split} \end{align*}

Divisão de frações

Na divisão, devemos multiplicar a primeira fração pelo inverso da segunda.

Exemplo 10

Como exemplo, vamos dividir a fração $7/a$ pela fração $3/a$:

\begin{align*} \begin{split} \frac{7}{a} / \frac{3}{a} &= \frac{ \ \frac{7}{a} \ }{ \ \frac{3}{a} \ } \\ &= \frac{7}{a} \cdot \frac{a}{3} \\ &= \frac{7 \cdot a}{a \cdot 3} \\ &= \frac{7 \cdot a}{3 \cdot a} \\ &= \frac{7}{3} \cdot \frac{a}{a} \\ &= \frac{7}{3} \cdot 1 \\ &= \frac{7}{3} \pt \end{split} \end{align*}

Exemplo 11

Vamos dividir a fração $3/4$ por $2$:

\begin{align*} \begin{split} \frac{3}{4} / 2 &= \frac{3}{4} \div \frac{2}{1} \\ &= \frac{ \ \frac{3}{4} \ }{ \ \frac{2}{1} \ } \\ &= \frac{3}{4} \cdot \frac{1}{2} \\ &= \frac{3}{8} \pt \end{split} \end{align*}

Exemplo 12

Vamos dividir o número $7$ pela fração $2/x$:

\begin{align*} \begin{split} 7 / \frac{2}{x} &= \frac{7}{1} \div \frac{2}{x} \\ &= \frac{ \ \frac{7}{1} \ }{ \ \frac{2}{x} \ } \\ &= \frac{7}{1} \cdot \frac{x}{2} \\ &= \frac{7x}{2} \pt \end{split} \end{align*}

Frações equivalentes

Ao multiplicarmos ou dividirmos os numerador e denominador de uma fração por um mesmo número, o resultado da fração não é alterado.

Exemplo 13

Neste exemplo, multiplicaremos o numerador e o denominador da fração $3/2$ por $5$:

\begin{equation*} \frac{3}{2} = \frac{3 \cdot 5}{2 \cdot 5} = \frac{15}{10} \pt \end{equation*}

E agora os dividiremos por $5$:

\begin{equation*} \frac{15}{10} = \frac{15/5}{10/5} = \frac{3}{2} \pt \end{equation*}

Você pode conferir que o resultado é mesmo:

\begin{equation*} \frac{3}{2} = \frac{15}{10} = 1{,}5 \pt \end{equation*}

Adição e subtração de frações

Para realizarmos somas e subtrações entre frações, devemos estar atentos a dois casos distintos: frações de denominadores iguais e frações de denominadores diferentes.

Denominadores iguais

Ao somarmos ou subtrairmos frações de mesmo denominador, devemos manter o denominador e prosseguir com a soma ou subtração dos numeradores.

Exemplo 14

Como exemplo, vamos somar a fração $7/5$ com a fração $2/5$:

\begin{align*} \begin{split} \frac{7}{5} + \frac{2}{5} &= \frac{7+2}{5} \\ &= \frac{9}{5} \pt \end{split} \end{align*}

Exemplo 15

Vamos subtrair a fração $9/y$ da fração $4/y$:

\begin{align*} \begin{split} \frac{4}{y} - \frac{9}{y} &= \frac{4-9}{y} \\ &= \frac{-5}{y} \\ &= -\frac{5}{y} \pt \end{split} \end{align*}

Denominadores diferentes

Se os denominadores forem diferentes, precisamos torná-los iguais. Para isso, podemos utilizar técnicas como a do mínimo múltiplo comum (MMC). Mas, como o foco aqui não é a matemática em si, seremos mais práticos se fizermos o uso de frações equivalentes.

Exemplo 16

Neste exemplo, para somar $\frac{3}{5}$ com $\frac{2}{10}$, multiplicaremos o numerador e o denominador da primeira fração por $2$.

\begin{align*} \frac{3}{5} + \frac{2}{10} &= \frac{3 \cdot 2}{5 \cdot 2} + \frac{2}{10} \\ &= \frac{6}{10} + \frac{2}{10} \\ &= \frac{6+2}{10} \\ &= \frac{8}{10} \end{align*}

Exemplo 17

Aqui, para operar $\frac{1}{a} - \frac{2}{b}$, precisaremos de um pouco mais de traquejo: vamos multiplicar o numerador e o denominador da primeira fração por $b$ e os da segunda fração por $a$.

\begin{align*} \frac{1}{a} - \frac{2}{b} &= \frac{1 \cdot b}{a \cdot b} - \frac{2}{b} \\ &= \frac{b}{ab} - \frac{2}{b} \\ &= \frac{b}{ab} - \frac{2 \cdot a}{b \cdot a} \\ &= \frac{b}{ab} - \frac{2a}{ab} \\ &= \frac{b-2a}{ab} \end{align*}

Palavras finais

Agora você já deve ser capaz de resolver problemas de física que envolvem frações. Para isso, lembre-se de que é importante respeitar a ordem de prioridade das operações.

Você também pode fixar o que foi abordado nesse resumo resolvendo alguns exercícios sobre frações. Bons estudos.

---

Próximo resumo >

☰ Índice de resumos

< Resumo anterior

---