Geometria básica (resumo nível médio)

Fonte: imagem gerada com IA no DALL·E.

Sim, geometria também é um pré-requisito para física. Neste resumo recordaremos algumas formas geométricas simples e algumas de suas propriedades.

Ângulo

Na matemática, ângulo é a medida da abertura formada no encontro de duas retas.

Figura 1. Representação de um ângulo (em vermelho) formado pelo encontro de duas retas (em preto).

Seu valor pode ser dado em grau ($\gr$) ou em radiano ($\mathrm{rad}$). Quando dado em radiano, é comum a utilização de $\pi$, cujo valor aproximado é $3{,}14$, isto é, $\pi \approx 3{,}14$.

Animação 1. Valores angulares variando de $45\gr$ em $45\gr$. Convencionou-se a utilização do sentido anti-horário como positivo.

Na Animação 1 podemos observar alguns valores de ângulos entre uma reta horizontal fixa e uma outra reta que está variando de $45\gr$ em $45\gr$ (ou de $\pi/4 \ \mathrm{rad}$ em $\pi/4 \ \mathrm{rad}$).

Por conveniência, ou padronização, mede-se ângulos no sentido anti-horário; ângulos medidos no sentido horário são negativos. Como exemplo, $-90\gr = 270\gr$, $45\gr = -315\gr$ e $-180\gr = 180\gr$ (faça um rascunho no papel para conferir).

Note que uma volta completa é obtida quando se atinge $360\gr$ (o equivalente a $2\pi \ \mathrm{rad}$) e, a partir disso, teremos ângulos equivalentes, tudo se repete. Ou seja, ângulos maiores que $360\gr$ são ângulos que já completaram pelo menos uma volta.

Exemplo 1

No skate, a manobra aérea chamada de 900 consiste em girar $900\gr$ no ar. O ângulo $900\gr$ pode ser reescrito como $360\gr + 360\gr + 180\gr$, isto é, duas voltas completas mais meia volta.

A conversão entre grau e radiano pode ser feita através da regra de três direta, onde, por exemplo, sabe-se que $360\gr$ equivale a $2\pi \ \mathrm{rad}$.

Paralelismo

Duas retas são paralelas se elas estiverem na mesma direção, isto é, se o ângulo entre elas for equivalente a $0\gr$.

Figura 2. Duas retas paralelas.

Na Figura 2 podemos observar duas retas paralelas. Se nós as sobrepusermos, uma em cima da outra, veremos que o ângulo entre elas é equivalente a $0\gr$.

Perpendicularidade

Duas retas são perpendiculares (também chamadas de normais ou ortogonais) se o ângulo entre elas for equivalente a $90\gr$.

Figura 3. Ângulo reto (em vermelho) formado pelo encontro de duas retas perpendiculares (em preto).

Qualquer ângulo equivalente a $90\gr$ é chamado de ângulo reto e comumente representado por $⊡$, como ilustrado na Figura 3.

Retângulo

Retângulo é a figura geométrica formada por quatro retas — quatro lados — e quatro ângulos retos e, por isso, os lados opostos são sempre iguais.

Figura 4. Retângulo com lados de comprimentos $a$ (em azul) e $b$ (em verde) e área $A$ (em vermelho).

Dado um retângulo com lados de comprimentos $a$ e $b$, como o da Figura 4, o perímetro (contorno) $p$ que o delimita é a soma dos lados,

\begin{align} \begin{split} p &= a + b + a + b \\ &= 2(a+b) \vg \end{split} \end{align}

e a área $A$, que é o tamanho da região interna, é o produto do lado menor com o lado maior,

\begin{equation} A = ab \pt \end{equation}

Quadrado

Um quadrado é um retângulo com lados de comprimentos iguais.

Figura 5. Quadrado de lados $l$ (em preto) e área $A$ (em vermelho).

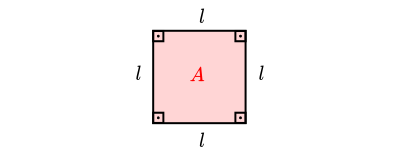
Dado um quadrado de lados $l$, como o da Figura 5, o perímetro $p$ que o delimita é

\begin{align} \begin{split} p &= l + l + l + l \\ &= 4l \vg \end{split} \end{align}

e a área $A$, que é o tamanho da região interna, é

\begin{align} \begin{split} A &= ll \\ &= l^2 \pt \end{split} \end{align}

Triângulo

Um triângulo é uma figura geométrica formada por três retas — três lados — e três ângulos.

Figura 6. Exemplo de um triângulo de base $b$, altura $h$, área $A$ e ângulos internos iguais a $\alpha$, $\beta$ e $\theta$.

A soma dos ângulos internos de qualquer triângulo deve resultar em $180\gr$. Assim, dado um triângulo de ângulos internos $\alpha$, $\beta$ e $\theta$, como o da Figura 6, temos:

\begin{equation} \alpha + \beta + \theta = 180\gr \pt \end{equation}

Ainda, a área de um triângulo é metade do produto da base pela altura. Se a base do triângulo for $b$ e a altura for $h$, a área $A$ do triângulo é

\begin{equation} A = \frac{bh}{2} \pt \end{equation}

Círculo

Um círculo é uma figura geométrica que não possui lados nem ângulos. Ele é comumente caracterizado pelo raio, que é a distância do centro até a borda, ou pelo diâmetro, que é duas vezes a distância do raio.

Figura 7. Círculo de raio $r$ (em azul), diâmetro $d$ (em verde) e área $A$ (em vermelho).

O perímetro (também chamado de contorno ou circunferência) $p$ de um círculo de raio $r$, ou diâmetro $d$, como o da Figura 7, pode ser calculado através de

\begin{align} \begin{split} p &= 2 \pi r \\ &= \pi d \vg \end{split} \end{align}

e a sua área $A$ pode ser calculada através de

\begin{align} \begin{split} A &= \pi r^2 \\ &= \pi \frac{d^2}{4} \pt \end{split} \end{align}

Palavras finais

Você pode testar seus conhecimentos resolvendo alguns exercícios de geometria relacionados a esse resumo. Bons estudos.

---

Próximo resumo >

☰ Índice de resumos

< Resumo anterior

---