Trigonometria básica (resumo nível médio)

Fonte: imagem gerada com IA no DALL·E.

Trigonometria é um tópico da matemática que estuda o triângulo retângulo. Neste resumo, relembraremos algumas propriedades trigonométricas interessantes.

Triângulo retângulo

Um triângulo é retângulo quando um de seus ângulos é reto. O maior dos lados do triângulo retângulo, que é sempre oposto ao ângulo reto, é chamado de hipotenusa; os outros dois lados são chamados de catetos.

Na Figura 1 temos a representação de um triângulo retângulo cuja hipotenusa possui comprimento $h$, um dos catetos possui comprimento $a$ e o outro cateto possui comprimento $b$.

Figura 1. Triângulo retângulo. Em azul, o lado de comprimento $a$ é o cateto oposto ao ângulo $\alpha$; em verde, o lado de comprimento $b$ é o cateto oposto ao ângulo $\beta$; e, em vermelho, a hipotenusa de comprimento $h$ é oposta ao ângulo reto.

Como dito anteriormente, a soma dos ângulos internos de qualquer triângulo deve sempre resultar em $180\gr$. No caso do triângulo retângulo, temos:

\begin{equation} \alpha + \beta = 90\gr \pt \end{equation}

Teorema de Pitágoras

O teorema de Pitágoras estabelece que, num triângulo retângulo, o quadrado da hipotenusa é igual à soma do quadrado dos catetos. Ou seja, com relação ao triângulo da Figura 1,

\begin{equation} h^2 = a^2 + b^2 \pt \end{equation}

A relação acima é útil quando temos os valores dos comprimentos de dois lados e desejamos saber o valor do comprimento do terceiro lado.

Razões trigonométricas

Dado um triângulo retângulo, há três razões trigonométricas fundamentais que relacionam um ângulo com dois dos lados: o seno, o cosseno e a tangente.

Seno

O seno de um ângulo é dado pela razão entre o cateto oposto a esse ângulo e a hipotenusa.

\begin{equation} \txt{seno} = \frac{\txt{cateto oposto}}{\txt{hipotenusa}} \end{equation}

No caso do triângulo da Figura 1,

\begin{equation} \sin{\alpha} = \frac{a}{h} \end{equation}

e

\begin{equation} \sin{\beta} = \frac{b}{h} \pt \end{equation}

Vale a pena ressaltar que o seno de um ângulo real nunca será menor que $-1$ nem maior que $1$.

Cosseno

O cosseno de um ângulo é dado pela razão entre o cateto adjacente a esse ângulo e a hipotenusa.

\begin{equation} \txt{cosseno} = \frac{\txt{cateto adjacente}}{\txt{hipotenusa}} \end{equation}

Voltando à Figura 1,

\begin{equation} \cos{\alpha} = \frac{b}{h} \end{equation}

e

\begin{equation} \cos{\beta} = \frac{a}{h} \pt \end{equation}

Assim como o seno, o cosseno de um ângulo real nunca será menor que $-1$ nem maior que $1$.

Tangente

A tangente de um ângulo é dada pela razão entre o cateto oposto e o cateto adjacente a esse ângulo, é o mesmo que dividir o seno pelo cosseno.

\begin{align} \begin{split} \txt{tangente} &= \frac{\txt{seno}}{\txt{cosseno}} \\ &= \frac{\txt{cateto oposto}}{\txt{cateto adjacente}} \end{split} \end{align}

Da Figura 1,

\begin{align} \begin{split} \tan{\alpha} &= \frac{\sin{\alpha}}{\cos{\alpha}} \\ &= \frac{a}{b} \end{split} \end{align}

e

\begin{align} \begin{split} \tan{\beta} &= \frac{\sin{\beta}}{\cos{\beta}} \\ &= \frac{b}{a} \pt \end{split} \end{align}

Em contrapartida com o seno e o cosseno, a tangente de um ângulo real pode resultar em qualquer valor real.

Ângulos notáveis

Há alguns ângulos cujos senos, cossenos e tangentes são amplamente conhecidos e utilizados. Por isso, é importante conhecê-los.

Tabela 1. Ângulos notáveis.

	$0\gr$	$30\gr$	$45\gr$	$60\gr$	$90\gr$
$\sin$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$
$\cos$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$
$\tan$	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	-

Os ângulos da Tabela 1 são os que aparecem com mais frequência. Outros valores podem aparecer; mas por sorte, na maioria das vezes, os enuncuados de problemas de física contêm as informações necessárias para resolvê-los.

Lei dos cossenos

Dado um triângulo qualquer de lados $a$, $b$ e $c$, com apenas um de seus ângulos conhecido, $\theta$, como o da Figura 2, temos a seguinte relação entre esse ângulo e os três lados:

Figura 2. Triângulo de lados $a$, $b$ e $c$, com um único ângulo conhecido, $\theta$.

\begin{equation} c^2 = a^2 + b^2 -2ab \cos{\theta} \pt \end{equation}

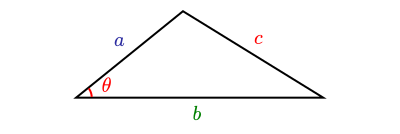
Note que, no caso em que $\theta = 90\gr$, o triângulo da Figura 2 se transforma num triângulo retângulo: o lado $c$ se transforma na hipotenusa e a Equação (12) se reduz ao teorema de Pitágoras pois, da Tabela 1, $\cos{(90\gr)} = 0$.

Palavras finais

Trigonometria é um assunto muito mais amplo do que o apresentado neste resumo. É melhor deixarmos toda essa vastidão e complexidade nas mãos de um professor de matemática, 😁.

Você pode resolver alguns exercícios de trigonometria para assimilar o que foi abordado nesse resumo. Bons estudos.

---

Próximo resumo >

☰ Índice de resumos

< Resumo anterior

---