Produtos com vetores (resumo nível médio)

Fonte: imagem criada no Canva.

Por possuir orientação, os vetores não podem ser operados como números comuns. Em vista disso, após o resumo sobre vetores vimos algumas maneiras de se lidar com a soma entre vetores.

Neste resumo, apresentaremos três tipos de produtos que envolvem vetores: a multiplicação por um número, o produto escalar e o produto vetorial.

Multiplicação por um número

Multiplicar um vetor por um número qualquer, ato também conhecido como multiplicação por um escalar, resulta na alteração dos comprimento e sentido do vetor. A direção não se altera.

Ao multiplicarmos um vetor $\vec{v}$ por um número $k$, obteremos um vetor resultante $\vec{R}$ que pode ser escrito como

\begin{equation} \vec{R} = k \vec{v} \pt \end{equation}

O módulo do vetor resultante é simplesmente o produto do módulo do número $k$ com o módulo de $\vec{v}$:

\begin{align} \begin{split} \lvert \vec{R} \rvert &= \lvert k\vec{v} \rvert \\ &= \lvert k \rvert \, \lvert \vec{v} \rvert \pt \end{split} \end{align}

Então, um vetor negativo pode ser interpretado como o produto de um vetor pela constante $k=-1$. Por exemplo, $\vec{a}=-\vec{g}$ é o mesmo que $\vec{a}=-1\vec{g}$, e isso significa que $\vec{a}$ e $\vec{g}$ possuem os mesmos módulo e direção, mas o sentido de um é oposto ao sentido do outro.

Nesse sentido, a subtração entre vetores é uma soma vetorial onde ao menos um dos vetores é negativo.

Assim, a subtração entre dois vetores iguais resulta no vetor nulo. Da mesma forma, o produto de um vetor qualquer pelo número $0$ também resulta no vetor nulo.

Exemplo 1

Se $\vec{a}$ é um vetor qualquer,

\begin{equation*} \vec{a}-\vec{a} = \vec{0} \end{equation*}

e

\begin{equation*} 0\vec{a}= \vec{0} \pt \end{equation*}

Exemplo 2

Considere os vetores da figura abaixo onde o vetor $\vec{a}$ possui módulo $\lvert \vec{a} \rvert = 2 \ \mathrm{un}$.

Figura 1-1. Ilustração da multiplicação de um vetor $\vec{a}$ pelos números $2$, $-1{,}5$ e $0{,}5$.

Na Figura 1-1 podemos observar três exemplos da multiplicação de um vetor $\vec{a}$ por um número. O vetor $\vec{b}=2\vec{a}$ tem módulo $\lvert \vec{b} \rvert$ $ = \lvert 2 \cdot 2 \rvert $ $ = 4 \ \mathrm{un}$. O vetor $\vec{c}=-1{,}5\vec{a}$ tem módulo $\lvert \vec{c} \rvert$ $ = \lvert -1{,}5 \cdot 2 \rvert $ $ = 3 \ \mathrm{un}$. E, por fim, o vetor $\vec{d}=0{,}5\vec{a}$ tem módulo $\lvert \vec{d} \rvert$ $ = \lvert 0{,}5 \cdot 2 \rvert $ $ = 1 \ \mathrm{un}$.

Produto escalar

O produto escalar entre dois vetores é igual ao produto de seus módulos com o cosseno do ângulo formado entre eles. O resultado é sempre um número, e não um vetor.

Figura 1. Representação do ângulo formado por dois vetores.

Dado dois vetores $\vec{a}$ e $\vec{b}$, como os da Figura 1, com $\theta$ sendo o ângulo entre eles, o produto escalar de $\vec{a}$ com $\vec{b}$ é um número que pode ser escrito como

\begin{equation} \vec{a} \cdot \vec{b} = \lvert \vec{a} \rvert \lvert \vec{b} \rvert \cos{\theta} \vg \end{equation}

onde devemos obrigatoriamente colocar o ponto $\cdot$ entre os vetores.

Ainda, é interessante notar que, no produto escalar, a ordem da operação não importa, ou seja,

\begin{equation} \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \pt \end{equation}

Produto vetorial

O produto vetorial entre dois vetores resulta em um novo vetor. O módulo desse produto é calculado através do produto dos módulos dos dois vetores com o seno do ângulo formado entre eles.

Figura 2. Em (a) temos uma representação do produto vetorial entre os vetores $\vec{a}$ e $\vec{b}$. O resultado do produto vetorial $\vec{a} \times \vec{b}$ é o vetor representado em azul. Em (b) temos o mesmo mas com uma visão em perspectiva.

Dado dois vetores $\vec{a}$ e $\vec{b}$, como os da Figura 2, o produto vetorial de $\vec{a}$ com $\vec{b}$ é designado por $\vec{a} \times \vec{b}$, onde devemos obrigatoriamente colocar o símbolo $\times$ entre os vetores. O módulo desse produto pode ser calculado como

\begin{equation} \lvert \vec{a} \times \vec{b} \rvert = \lvert \vec{a} \rvert \lvert \vec{b} \rvert \sin{\theta_{ab}} \vg \end{equation}

onde $\theta_{ab}$ é o ângulo que vai do vetor $\vec{a}$ ao $\vec{b}$, isto é, é o ângulo que parte do primeiro vetor e termina no segundo vetor.

O resultado do produto vetorial entre dois vetores é um novo vetor de direção perpendicular a eles. Sua orientação é determinada através da regra da mão direita, como veremos a seguir.

Regra da mão direita

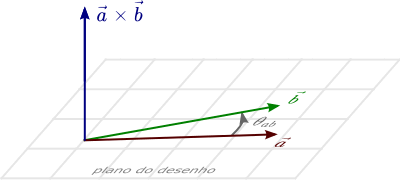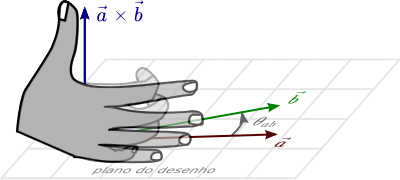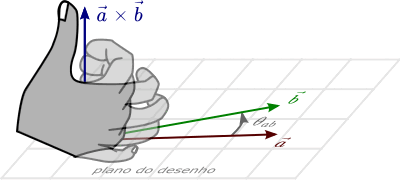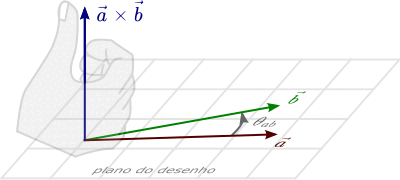
A regra da mão direita, utilizada em produtos vetoriais, consiste em orientarmos nossos dedos indicador, médio, anelar e mínimo na direção do primeiro vetor, e fecharmos a mão acompanhando o ângulo que vai do primeiro para o segundo vetor. A orientação do produto vetorial é igual à do polegar.

Na Animação 1, podemos ver uma exemplificação da aplicação da regra da mão direita no produto vetorial entre os vetores $\vec{a}$ e $\vec{b}$. O resultado é um vetor $\vec{a} \times \vec{b}$ que sai do plano do desenho.

Animação 1. Regra da mão direita na determinação da orientação do vetor resultante do produto vetorial entre os vetores $\vec{a}$ e $\vec{b}$.

No produto vetorial, a ordem da operação é muito importante. Você pode conferir, de maneira análoga à Animação 1, que ao realizarmos o produto vetorial de $\vec{b}$ com $\vec{a}$, ou seja, $\vec{b} \times \vec{a}$, o resultado terá sentido invertido (o polegar estará entrando no plano do desenho). Portanto,

\begin{equation} \vec{a} \times \vec{b} = - \vec{b} \times \vec{a} \pt \end{equation}

Palavras finais

Os produtos escalar e vetorial são pouco abordados em conteúdos de nível médio. Por isso, o que foi apresentado, além de não ter muita aplicação aparente, pode ser um assunto novo para muitos estudantes. Não se preocupe, você não precisará se aprofundar nesses assuntos.

Entretanto, se quiser saber mais sobre vetores, vale a pena assistir o Episódio 5, entitulado "Vetores", da série "O Universo Mecânico" (The Mechanical Universe... and Beyond, 1985) produzida pelo Instituto de Tecnologia da Califórnia (Caltech). Apesar de ser antigo, é didático e pode ser facilmente encontrado na internet.

Por fim, aproveite para assimilar este resumo resolvendo a lista de exercícios sobre produtos com vetores. Bons estudos.

---

☰ Índice de resumos

< Resumo anterior

---